Application of Extended Fuzzy ISOCOV Methodology in Nanomaterial Selection Based on Performance Measures
Abstract:
The prevalence of decision-making methodologies catering to quantitative attributes considerably overshadows those designed for qualitative attributes. This study seeks to address this gap by extending the traditional Ideal Solutions with Constraint on Values (ISOCOV) method to a fuzzy environment, thereby enhancing its capability to handle optimal decision-making based on qualitative attributes. In this improved method, $\alpha$-cut representations are employed for managing linguistic value constraints in performance-oriented data. The proposed approach is then utilized for the selection of nanomaterials, evaluated based on five essential criteria. By subjecting the performance-based decision matrix to the modified fuzzy method, a ranking of alternatives is derived. Compared to its traditional counterpart, this fuzzy-enhanced ISOCOV method demonstrates enhanced efficiency in processing qualitative data, promising its potential compatibility and utility for decision makers dealing with performance-oriented decision-making.
1. Introduction
Nanomaterials, with their dimensions on the order of 10-9 meters, are renowned for their high chemical reactivity and the quantum effects that they display, traits that make them particularly suitable for commercial product development. Though these materials can be found in nature, they are often synthesized through various techniques, including decomposition and combustion methods [1], [2], [3].
These materials, classified as organic, inorganic, carbon-based, and composite, have found widespread application across diverse fields. One of their key features is their remarkable compatibility with different optical, chemical, electrical, mechanical, and magnetic properties, which have led to their incorporation in a variety of industries, including electrical, medical, automotive, aerospace, and cosmetics, among others [4], [5], [6].
Upon close examination, it is evident that the internal and external structural physiochemical properties of nanomaterials stand distinct and robust in comparison to other types of materials. However, despite their utility, the proliferation of different types of nanomaterials and the multitude of their synthesis methods have posed challenges. Additionally, concerns around nanotoxicity further complicate decision-making processes in manufacturing [7], [8], [9].
The complexity of the decision-making landscape has led researchers to employ various multi-criteria decision-making methods to address nanomaterial-based problems. Grieger et al. [1], for example, tackled the decision-making process related to the health risks of nanomaterials in uncertain scenarios, while Mullin et al. [2] focused on risk governance in the field of nanotechnology. Landsiedel et al. [4] and Barry and Shatkin [3] contributed with a risk-based approach to decision-making concerning the safety and health aspects of nanomaterials and nanotechnology, respectively.
Numerous studies have aimed to integrate societal concerns in decision-making processes [5], devise models for policy decisions regarding nanomaterials [6], [7], and assess environmental impacts of nanomaterials [8], [9], [10], [11]. There are also contributions towards developing models for framing regulatory measures in nanomaterials [12] and analyzing the risk indicators associated with developing nanomaterials [13]. A number of researchers have focused on the production [14] and synthesis methods of nanomaterials [15], as well as decision-making methods for grouping nanomaterials [16], [17], [18]. Analytic hierarchy processes have been applied to fabricate nanomaterials [19], and decision models have been designed for optimal selection of carbon-based nanomaterials [20].
The literature thus demonstrates a significant application of decision-making approaches to problems related to the selection of nanomaterials, processing technology, risk indicators, environmental effects, and others. However, several gaps remain. For instance, there is a lack of decision-making models based on the performance measures of nanomaterials with respect to their properties, and the application of fuzzy-based multi-criteria decision-making methods in modelling is limited. Further research should aim to address these gaps and enhance the field's understanding of this complex decision-making landscape.
The genesis of this study is firmly rooted in the application of the ISOCOV method in decision-making models based on performance measures of nanomaterials, which is proposed by Abdelli et al. [21] in the crisp sense, incorporating the concept of value constraints. This methodology shares notable links with TOPSIS and VIKOR when it comes to generating an ideal solution. Previously, the ISOCOV method was primarily applied to decisions concerning web services, yet the existing literature regarding its applications remains somewhat sparse.
The practicality of this method lies in its consideration of extreme values of alternatives alongside the constraint values of criteria. However, it's worth noting that the values considered are quantitatively focused. Upon closer examination, it's clear that managing decision-making data based solely on quantitative measures and establishing quantitative constraint values isn't always viable. More often than not, decision-makers are tasked with managing performance-based measures.
This situation thus catalyzed the expansion of the crisp ISOCOV method to a fuzzy-based approach, which better accommodates qualitative data and linguistic representations of constraint values. This study develops Fuzzy ISOCOV to determine optimal solutions to the decision-making problem regarding nanomaterial selection, considering performance measures related to five different properties of nanomaterials: optic, mechanical, chemical, electrical, and magnetic.
This manuscript is divided into distinct sections for ease of understanding. The second section details the steps involved in Fuzzy ICOSOV. The third section applies this proposed methodology to nanomaterial selection, followed by a discussion of results in section four. The manuscript concludes with final remarks and the broader implications of the work in the last section.
2. Fuzzy ICOSOV
This section delineates the procedural steps involved in the implementation of the novel method, Fuzzy Ideal Solutions with Constraint on Values (Fuzzy ICOSOV), designed specifically for handling qualitative data with linguistic constraint values.
Step 1: Defining decision making problem
In the first step, the decision-making problem is defined succinctly, drawing on the expertise of domain-specific specialists. This includes the designation of alternatives and criteria pertinent to the problem at hand. A decision matrix [$\mathrm{p}_{\mathrm{ij}}$] is subsequently developed, denoting an order of u × v, populated with performance scores represented as percentage values.
Step 2: Determination of criterion weights
The succeeding step encompasses the calculation of criterion weights. This process can be facilitated through the application of any suitable method, or, in the absence of any such preference, equal weights may be assigned.
Step 3: Constraint satisfaction values
The third stage of the process involves the calculation of constraint satisfaction values, employing trapezoidal fuzzy numbers to represent linguistic constraint values. This form $\left(T_1, T_2, T_3, T_4\right)$ is subsequently expressed via $\alpha$-cuts as $[a \alpha+b, c-a \alpha]$. In scenarios where $\alpha$ is set to 1, the 1-cut becomes $[\mathrm{a}+\mathrm{b}, \mathrm{c}-\mathrm{a}]=[\mathrm{x}, \mathrm{y}]$. The constraint satisfaction values $(\mathrm{CS})$ of each alternative are derived accordingly.
$C S=\left\{\begin{array}{c} 1 \quad \text { if } p_{i j} \in[x, y] \\ \frac{100-e}{100} \text { if }\left|p_{i j}-x\right| \leq e \\ \frac{100-e}{100} \text { if }\left|p_{i j}-y\right| \leq e \\ 0 \quad \text { if } p_{i j}=0 \end{array}\right.$
An array of alpha-cut values is utilized to denote the linguistic constraint values as trapezoidal fuzzy numbers, enabling decision-makers to make necessary adjustments to the constraint values.
Step 4: Normalization of the decision matrix
In the fourth step, the decision matrix formulated previously is normalized employing a vector normalization method.
$N_{i j}=\frac{p_{i j}}{\sum_{i=1}^u\left(p_{i j}\right)^2}$
Step 5: Weighted normalized matrix with constraint satisfaction value
The fifth stage includes the calculation of the weighted normalized matrix with the constraint satisfaction value. The normalized matrix values are multiplied with both the criterion weights, computed in step two, and the linguistic constraint satisfaction values. Therefore, $\mathrm{d}_{\mathrm{ij}}=\mathrm{N}_{\mathrm{ij}} \times \mathrm{w}_{\mathrm{j}} \times \mathrm{cs}$.
Step 6: Calculation of ideal solutions
In the sixth step, positive and negative ideal solutions (PI and NI) for each criterion are determined. For benefitbased criteria, $\mathrm{PI}=\mathrm{Max}\left\{\mathrm{d}_{\mathrm{ij}}\right\}, \mathrm{NI}=\mathrm{Min}\left\{\mathrm{d}_{\mathrm{ij}}\right\}$, for $\mathrm{i}=1$ to $\mathrm{u}$. Conversely, for non-benefit criteria, $\mathrm{PI}=\mathrm{Min}\left\{\mathrm{d}_{\mathrm{ij}}\right\}, \mathrm{NI}=\mathrm{Max}$ $\left\{\mathrm{d}_{\mathrm{ij}}\right\}$, for $\mathrm{i}=1$ to $\mathrm{u}$.
Step 7: Calculation of distance measures
The seventh stage entails the calculation of Euclidean distance measures from each alternative's PI and NI.
$E_i^{+}=\sqrt{\sum_{i=1}^v\left(P I-d_{i j}\right)^2}, E_i^{-}=\sqrt{\sum_{i=1}^v\left(N I-d_{i j}\right)^2}$
Step 8: Computations of closeness measures
In the final step, the closeness measure Ci is computed as follow
$\mathrm{C}_{\mathrm{i}}=\frac{E_i^{-}}{E_i^{-}+E_i^{+}}$
3. Application of Fuzzy ICOSOV in Nanomaterial Selection
In the section that follows, an application of the method delineated in Section 2, named Fuzzy ICOSOV, is presented. The procedure is specifically applied to the selection of nanomaterials, considering an array of distinctive properties as crucial benefit criteria. Ten nanomaterials are randomly selected as alternatives, with a constructed decision matrix displaying percentage score values indicating the degree to which each alternative meets the respective criteria.
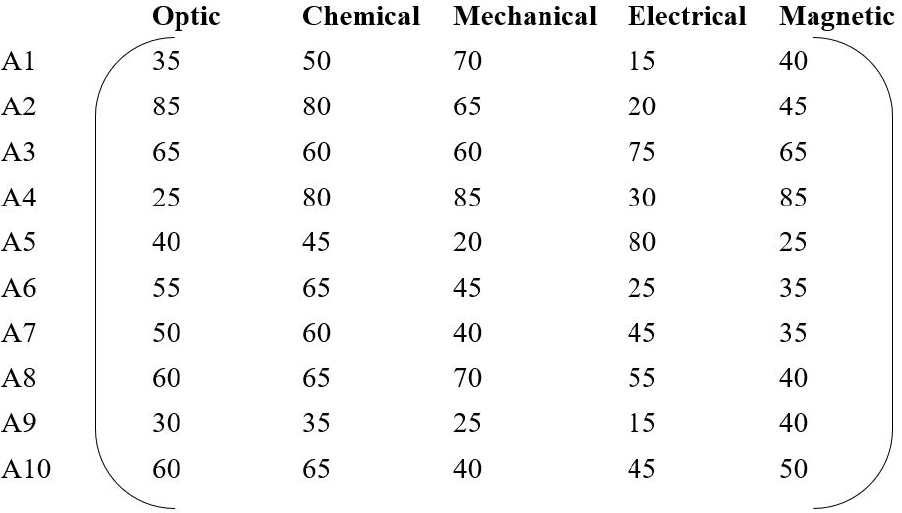
For the matrix, each cell entry symbolizes the performance measure, varying within the range of 0 to 100, highlighting the extent to which each alternative fulfills the set criteria. The weighting factor for each criterion (wj) is taken to be 0.2, indicating an assumption of equal importance across all criteria.
The normalized values of the matrix are as follows
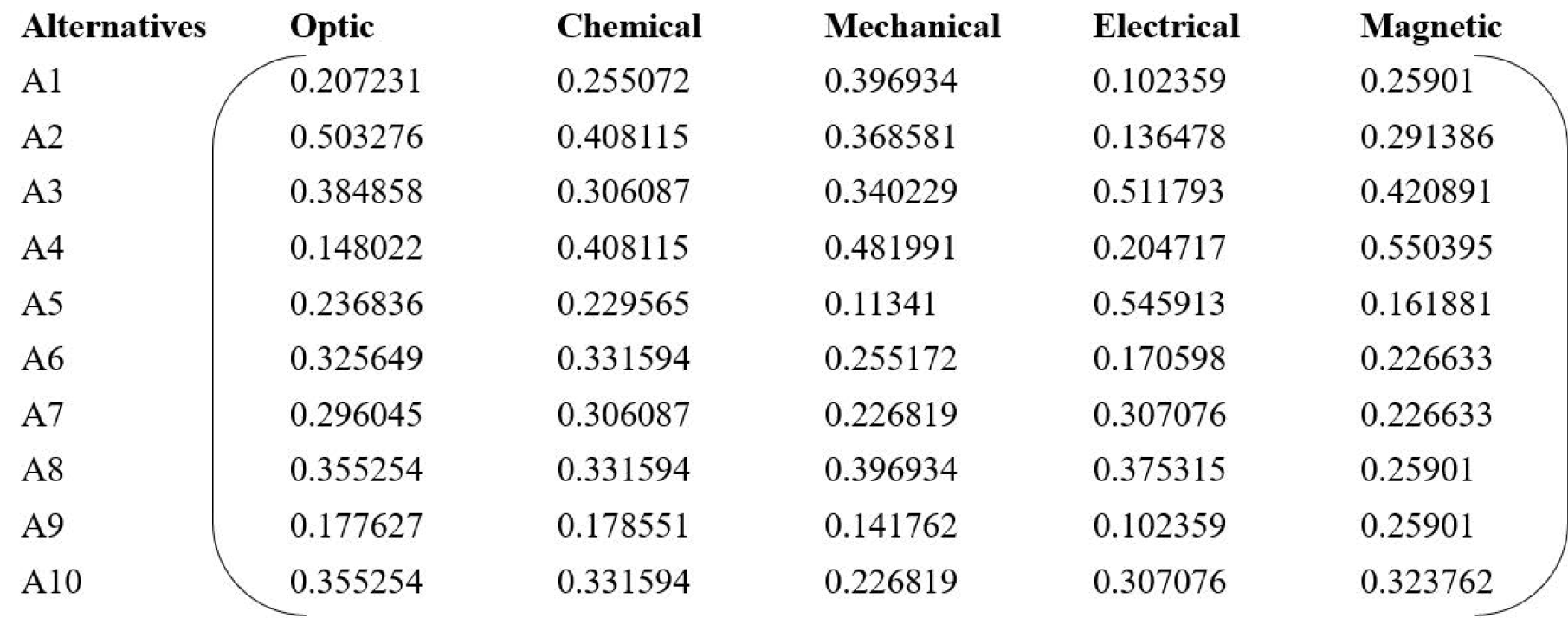
In the subsequent process, the normalization of the matrix was accomplished, whereupon constraint satisfaction values were assumed as linguistic variables. These variables are detailed in Table 1. Assumptions were made that the constraint value for the criteria is high, with the corresponding $\alpha$-cut delineated as $[10 \alpha+50,80-10 \alpha]$. In a scenario where $\alpha$ equals 1 , the result would be [60, 70]. Employing Step 3, the constraint satisfaction values (CS) were obtained, as presented in Table 2.
Linguistic Variable | Trapezoidal Fuzzy Number Representation | Alpha-cut Representation |
Very Low | (0,5,5,10) | [5α, 10 - 5α] |
Low | (10,20,30,40) | [10α + 10, 40 - 10α] |
Moderate | (30,40,50,60) | [10α + 30, 60 - 10α] |
High | (50,60,70,80) | [10α + 50, 80 - 10α] |
Very High | (80,90,90,100) | [10α + 80, 100 - 10α] |
Alternatives | Optic | Chemical | Mechanical | Electrical | Magnetic |
A1 | 0.75 | 0.9 | 0.9 | 0.55 | 0.8 |
A2 | 0.75 | 0.8 | 0.95 | 0.6 | 0.85 |
A3 | 0.95 | 1 | 1 | 0.85 | 0.95 |
A4 | 0.65 | 0.8 | 0.75 | 0.7 | 0.75 |
A5 | 0.8 | 0.85 | 0.6 | 0.8 | 0.65 |
A6 | 0.95 | 0.95 | 0.85 | 0.65 | 0.75 |
A7 | 0.9 | 1 | 0.8 | 0.85 | 0.75 |
A8 | 1 | 0.95 | 0.9 | 0.95 | 0.8 |
A9 | 0.7 | 0.75 | 0.65 | 0.55 | 0.8 |
A10 | 1 | 0.95 | 0.8 | 0.85 | 0.9 |
Progressing further, the weighted normalized matrix with constraint satisfaction values was determined, utilizing the process outlined in Step 5. Consequent calculations of the positive and negative ideal solutions were then conducted according to Step 6, the results of which are listed in Table 3. Utilizing Step 7, Euclidean measures were calculated, as seen in Table 4.
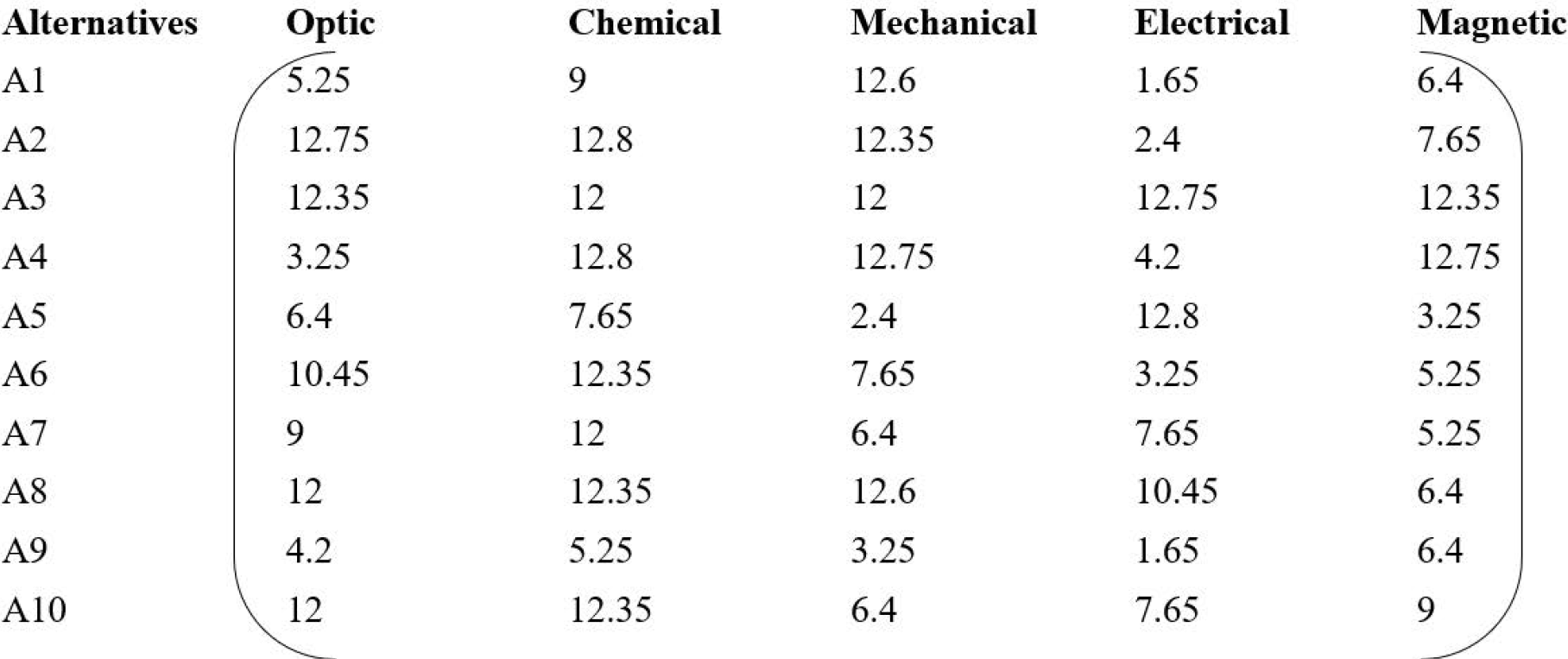
PI | 12.75 | 12.8 | 12.75 | 12.8 | 12.75 |
NI | 3.25 | 5.25 | 2.4 | 1.65 | 3.25 |
Alternatives | $\boldsymbol{E}_{\boldsymbol{i}}^{+}$ | $\boldsymbol{E}_{\boldsymbol{i}}^{-}$ |
A1 | 15.34137 | 11.49021 |
A2 | 11.59008 | 16.31495 |
A3 | 1.234909 | 20.65315 |
A4 | 12.81444 | 16.1517 |
A5 | 16.25477 | 11.83237 |
A6 | 13.37741 | 11.67786 |
A7 | 11.73872 | 11.6028 |
A8 | 6.828799 | 17.84307 |
A9 | 19.62142 | 3.398161 |
A10 | 9.037284 | 14.56142 |
In the final phase, closeness measures of the alternatives were calculated using Step 8, and rankings were made based on these final values, as displayed in Table 5. It is evident from Table 5 that the alternative A3 ranks as the ideal option, while A9 ranks as the least preferred. The other alternatives are ranked correspondingly, based on their scores.
Alternatives | $\boldsymbol{C}_{\boldsymbol{i}}$ | Rank |
A1 | 0.428235 | 8 |
A2 | 0.58466 | 5 |
A3 | 0.943581 | 1 |
A4 | 0.557606 | 4 |
A5 | 0.421274 | 9 |
A6 | 0.466084 | 7 |
A7 | 0.497089 | 6 |
A8 | 0.723215 | 2 |
A9 | 0.14762 | 10 |
A10 | 0.617043 | 3 |
4. Discussion
The investigation outlined herein contemplates a multi-faceted decision-making problem, initially approached with equal weights among criteria. This section re-evaluates the same issue, integrating differential criterion weights and varying alpha-cuts in order to derive the Constraint Satisfaction (CS) values. An established methodology, the Analytic Hierarchy Process (AHP), was employed for the computation of these criterion weights, as presented in Table 6.
Criteria | Optic | Chemical | Mechanical | Electrical | Magnetic |
Weights | 0.254 | 0.1524 | 0.2896 | 0.1243 | 0.1797 |
Alternatives | $\quad \boldsymbol{C}_{\boldsymbol{i}}$ | Rank |
A1 | 0.536482 | 6 |
A2 | 0.716239 | 3 |
A3 | 0.939504 | 1 |
A4 | 0.580365 | 5 |
A5 | 0.296876 | 9 |
A6 | 0.524427 | 7 |
A7 | 0.472004 | 8 |
A8 | 0.771757 | 2 |
A9 | 0.139074 | 10 |
A10 | 0.592683 | 4 |
As a result of the revised weighting scheme, final closeness values of the alternatives were calculated, and subsequent rankings were discerned, as displayed in Table 7. Remarkably, alternative A3 attained the highest ranking, while alternative A9 was found to be the least preferable. This ranking sequence aligns consistently with those produced under the previously applied equal weighting approach, evidenced by a high correlation coefficient value of 0.915.
Notwithstanding, the methodology was further extended by testing different alpha values, which are indicative of the extent to which the conditions for satisfying the constraints by the alternatives could be relaxed. Selection of the most suitable constraint value was determined based on the preferences and needs of the decision-makers.
In summary, this section has demonstrated that the adoption of differential criterion weights can offer a robust and adaptable approach for handling complex decision-making problems. The flexibility to adjust alpha values allows the decision-making process to remain adaptable to evolving constraints, thereby ensuring that optimal solutions are reached. This discussion affirms the validity of the employed methodology and its applicability to the decision-making scenario presented.
5. Conclusions
In the current study, a novel approach known as fuzzy ISOCOV has been proposed to manage linguistic constraint values and performance-based data. The versatility of this method becomes evident when applied to the task of selecting nanomaterials, which vary considerably in their properties. In this context, two scenarios have been analyzed in detail, one with equal weights assigned to the criteria and the other with unequal weights.
When the results of these scenarios are compared, striking similarities are observed, reinforcing the robustness of the proposed methodology. This approach can be effectively extended to environments that are intuitionistic and neutrosophic, thereby demonstrating its broad applicability. In future, it is crucial to achieve ideal optimal ranking outcomes through iterative refinement of the alpha values.
The significant role of the proposed method in decision-making processes cannot be understated, especially when dealing with performance-based datasets paired with linguistic constraints. By equipping decision-makers with such advanced tools, the possibility of more informed and accurate decisions can be enhanced.
In light of the knowledge generated from this study, it is suggested that future research should continue to expand on these findings. It may be worthwhile to investigate the impact of varying alpha values on the ranking outcomes in different application scenarios. Another direction could be to explore the efficiency of fuzzy ISOCOV when applied to other types of data or decision-making contexts. Furthermore, given the evident importance of linguistic constraints in decision-making, a deeper exploration of this area is also warranted.
These recommendations, while focused on the future, stem from the confidence in the efficacy of the proposed method, as demonstrated by the results of the current study. It is hoped that these insights will contribute to the broader scientific discourse on decision-making methodologies and their application in diverse fields.
The data used to support the findings of this study are available from the corresponding author upon request.
The authors declare that they have no conflicts of interest.
