Javascript is required
[1] Berger, B., Vorrichtung zum bediisen der oberflache eines bandes sowie bandbearbei- tungsanlage, October 18 2012. DE Patent App. DE201,110,002,017.
[2] Mohan Kumar, C., Elsen, P., Berger, B. & Janoske, U., Rotating impinging jets for surface cleaning of metals: Mathematical modeling and experimental investigation. Journal of Water Proc-cessing Engineering, Elsevier, submitted.
[3] Holmberg, K., A concept for friction mechanisms of coated surfaces. Surface and Coat- ing Technology, 56, pp. 1–10, 1992. [Crossref]
[4] Brackbill, J.U., Kothe, D.B. & Zemach, C., A continuum method for modeling surface tension. Journal of Computational Physics, 100(2), pp. 335–354, 1992. [Crossref]
[5] Berberovic, E., Hinsberg, N.V., Jakirlic, S., Roisman, I. & Tropea, C., Drop impact onto a liquid layer of finite thickness: Dynamics of the cavity evolution. Physical Review E, 79(3), 2009. [Crossref]
[6] Weller, H.G., A new approach to vof-based interface capturing methods for incompress- ible and compressible flows. Technical report, 2008.
[7] Hirt, C.W. & Nichols, B.D., Volume of fluid (VOF) method for the dynamics of free boundaries. Journal of Computational Physics, 39(1), pp. 201–225, 1981. [Crossref]
[8] Rusche, H., Computational fluid dynamics of dispersed two-phase flows at high phase fractions. PhD thesis, Imperial college of science, Technology and Medicine, London, 2002.
[9] Wilcox, D.C., Turbulence modeling for CFD. DCW Industries, Inc. c1994, La Cnada, CA, 1994.
[10] OpenFOAM Foundation. OpenFOAM C+ + Documentation.
[11] Georgiadou, M., Mohr, R. & Alkire, R.C., Local mass transport in two-dimensional cavities in laminar shear flow. Journal of The Electrochemical Society, 147(8), pp. 3021–3028, 2000.
Search

Acadlore takes over the publication of IJCMEM from 2025 Vol. 13, No. 3. The preceding volumes were published under a CC BY 4.0 license by the previous owner, and displayed here as agreed between Acadlore and the previous owner. ✯ : This issue/volume is not published by Acadlore.

Open Access
Research article

Numerical Modeling and Analysis of Viscous Media Removal from Grooved Surfaces with Rotating Impinging Jets

c. mohan kumar1,2,
p. elsen3,
b. berger4,
u. janoske1
1
University of Wuppertal, Germany
2
Baden-Wuerttemberg Cooperative State University, Mosbach, Germany
3
Breuer GmbH, Germany
4
Bernd-Berger Consulting, Germany
International Journal of Computational Methods and Experimental Measurements
|
Volume 4, Issue 4, 2016
|
Pages 573-582
Received: N/A,
Revised: N/A,
Accepted: N/A,
Available online: N/A
View Full Article|Download PDF

Abstract:

Surface cleaning prior to coating and fabrication processes is an important process to ensure the quality and proper functioning of the products. The current work involves the modeling of a cleaning process where viscous media is removed from surfaces using mechanical force from impinging water jets. The jets are mounted on a rotating nozzle carrier, which combine the normal force with increased tangential force resulting in the removal of oil present in the grooves of metal surfaces.

The modeling of such a process is performed with the volume of fluid (VOF) method with an open source Computational Fluid Dynamics (CFD) code Open-FOAM®. Rectangular grooves, which represent an idealized form of roughness are considered for numerical analysis. The oil present in the roughness grooves is resolved by the computational mesh.

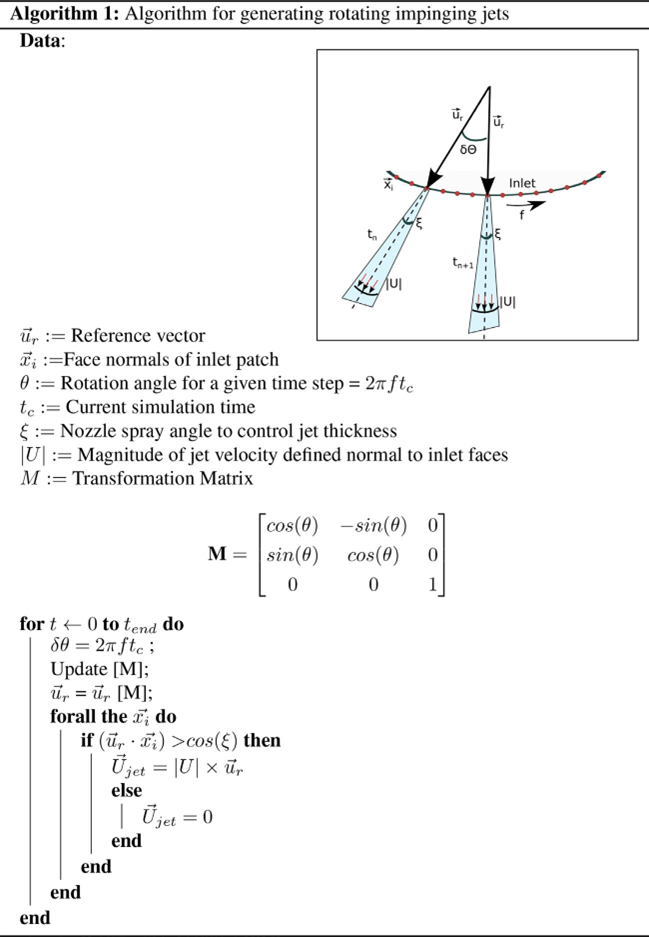
The inlet is modified to model the phenomenon of rotating jets. In order to model the effect of rotating jets, a reference vector is transformed by a time-dependent rotational tensor. All the faces which make a certain angle (opening angle) with the reference vector are activated. This results in the formation of jets with a thickness which can be controlled by the opening angle. The numerical model is used to study the influence of the frequency of rotation, nozzle exit velocity, viscosity of oil and the aspect ratio of the grooves on surface cleaning. An impinging turbulent jet is modeled using the k-epsilon turbulence model.

Finally, the CFD simulations are qualitatively compared with a previously developed semi-empirical model and experiments conducted in an industrial setup. The tendencies of oil removal due to the effect of the process parameters observed in the simulation are in close agreement with the semi-empirical model and experimental results. Thus, the cleaning model can be used to conduct sensitivity analysis to achieve an optimal performance of the cleaning process.

Keywords: CFD, Jets, Surface cleaning, Volume of fluid

1. Introduction

2. Modeling of the Cleaning Process

3. Numerical Simulation and Case Setup

4. Results and Discussion

5. Conclusions

Acknowledgments

The current work with the serial number KF2168632SU3 is financially supported by the Federal Ministry for Economic Affairs and Energy under Arbeitsgemein-schaft Industrieller Forschungsvereinigungen (AIF), Berlin in correspondence with the decision made by the Federal government of Germany.

References
[1] Berger, B., Vorrichtung zum bediisen der oberflache eines bandes sowie bandbearbei- tungsanlage, October 18 2012. DE Patent App. DE201,110,002,017.
[2] Mohan Kumar, C., Elsen, P., Berger, B. & Janoske, U., Rotating impinging jets for surface cleaning of metals: Mathematical modeling and experimental investigation. Journal of Water Proc-cessing Engineering, Elsevier, submitted.
[3] Holmberg, K., A concept for friction mechanisms of coated surfaces. Surface and Coat- ing Technology, 56, pp. 1–10, 1992. [Crossref]
[4] Brackbill, J.U., Kothe, D.B. & Zemach, C., A continuum method for modeling surface tension. Journal of Computational Physics, 100(2), pp. 335–354, 1992. [Crossref]
[5] Berberovic, E., Hinsberg, N.V., Jakirlic, S., Roisman, I. & Tropea, C., Drop impact onto a liquid layer of finite thickness: Dynamics of the cavity evolution. Physical Review E, 79(3), 2009. [Crossref]
[6] Weller, H.G., A new approach to vof-based interface capturing methods for incompress- ible and compressible flows. Technical report, 2008.
[7] Hirt, C.W. & Nichols, B.D., Volume of fluid (VOF) method for the dynamics of free boundaries. Journal of Computational Physics, 39(1), pp. 201–225, 1981. [Crossref]
[8] Rusche, H., Computational fluid dynamics of dispersed two-phase flows at high phase fractions. PhD thesis, Imperial college of science, Technology and Medicine, London, 2002.
[9] Wilcox, D.C., Turbulence modeling for CFD. DCW Industries, Inc. c1994, La Cnada, CA, 1994.
[10] OpenFOAM Foundation. OpenFOAM C+ + Documentation.
[11] Georgiadou, M., Mohr, R. & Alkire, R.C., Local mass transport in two-dimensional cavities in laminar shear flow. Journal of The Electrochemical Society, 147(8), pp. 3021–3028, 2000.
Cite this:
APA Style
IEEE Style
BibTex Style
MLA Style
Chicago Style
GB-T-7714-2015
Kumar, C. M., Elsen, P., Berger, B., & Janoske, U. (2016). Numerical Modeling and Analysis of Viscous Media Removal from Grooved Surfaces with Rotating Impinging Jets. Int. J. Comput. Methods Exp. Meas., 4(4), 573-582. https://doi.org/10.2495/CMEM-V4-N4-573-582
C. M. Kumar, P. Elsen, B. Berger, and U. Janoske, "Numerical Modeling and Analysis of Viscous Media Removal from Grooved Surfaces with Rotating Impinging Jets," Int. J. Comput. Methods Exp. Meas., vol. 4, no. 4, pp. 573-582, 2016. https://doi.org/10.2495/CMEM-V4-N4-573-582
@research-article{Kumar2016NumericalMA,
title={Numerical Modeling and Analysis of Viscous Media Removal from Grooved Surfaces with Rotating Impinging Jets},
author={C. Mohan Kumar and P. Elsen and B. Berger and U. Janoske},
journal={International Journal of Computational Methods and Experimental Measurements},
year={2016},
page={573-582},
doi={https://doi.org/10.2495/CMEM-V4-N4-573-582}
}
C. Mohan Kumar, et al. "Numerical Modeling and Analysis of Viscous Media Removal from Grooved Surfaces with Rotating Impinging Jets." International Journal of Computational Methods and Experimental Measurements, v 4, pp 573-582. doi: https://doi.org/10.2495/CMEM-V4-N4-573-582
C. Mohan Kumar, P. Elsen, B. Berger and U. Janoske. "Numerical Modeling and Analysis of Viscous Media Removal from Grooved Surfaces with Rotating Impinging Jets." International Journal of Computational Methods and Experimental Measurements, 4, (2016): 573-582. doi: https://doi.org/10.2495/CMEM-V4-N4-573-582
KUMAR C M， ELSEN P， BERGER B， et al. Numerical Modeling and Analysis of Viscous Media Removal from Grooved Surfaces with Rotating Impinging Jets[J]. International Journal of Computational Methods and Experimental Measurements， 2016， 4(4)： 573-582. https://doi.org/10.2495/CMEM-V4-N4-573-582